OPLOSSING (1)
Omdat tafelschikkingen zich het best laten visualiseren in een matrix heb ik –mbv VisualBasic- een programma in Excel ontwikkeld.
(Zie figuur hierboven) Na noodzakelijke input van aantal deelnemers, voorkeursgerechten, vrijstellingen, maximale tafelbezetting en gewenste roulatie (per koppel of individueel), wordt eerst bekeken of er wel een oplossing mogelijk is waarbij niemand elkaar 2x tegenkomt. De kans hierop wordt groter naarmate de verhouding van de som van het totaal aantal gerechten (aantal gastheren/vrouwen) en de som van het max.aantal koppels (of deelnemers bij individueel running dinner) per gerechtsoort groter wordt (Q in formule links). Als deze verhouding kleiner is dan 1, dan vindt het programma geen oplossing. Oorzaak kan zijn dat er te weinig gastheren en/of teveel vrijstellingen zijn ingevoerd.

Bij kleine waarden van Q (wel >1) zal het programma meer (reken)tijd nodig hebben om tot een passende oplossing te komen.

help3
 Na berekening van het noodzakelijk aantal gastheren voor elke gerechtsoort (keuze tussen 2, 3 of 4) worden eerst de gerechten verdeeld en vervolgens de aantallen gasten toegewezen. Hierbij wordt rekening gehouden met in het verleden toegewezen gerechten en evt. restricties wat betreft het max. aantal gasten aan tafel.

Bij de vulling van de horizontale gastheerregel wordt ook weer rekening gehouden met tafelschikkingen uit het verleden: er wordt gezocht naar gasten die nog nooit of het minst bij de gastheer aan tafel hebben gezeten.

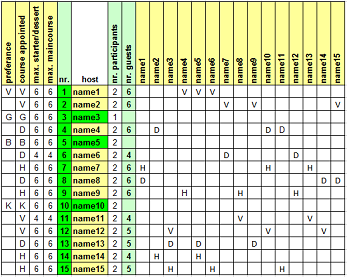
In de figuur bovenaan in kolom 2 vindt het programma een oplossing voor 14 koppels en 1 individu; deze (name3) is van een gerecht vrijgesteld, alsmede naam 5 en 10 die respectievelijk de borrel en koffie verzorgen. Naam1 wilde persé een Voorgerecht. Groen gearceerde namen zijn vrijgesteld van een gerecht.

NAAR DOWNLOAD.